Number Models:

Interactive Models

for Understanding Elementary Mathematics

Introduction

The purpose of this site is to create interactive models that can help

illustrate some of the concepts and methods of elementary

mathematics. The germ of the idea for me goes back to a cross-country

road trip I took with my family in 1956 when I was eight years

old. Between stops there were seemingly interminable periods of

boredom. During these periods, I found myself watching the dashboard,

specifically the odometer and speedometer, of the car, calculating how

much progress we were making toward our next stop and estimating when

we would get there.

The odometer in those days consisted of a set of

wheels marked in units of one-tenth of a mile. A unit of the next

represented a single mile of progress, the units of the next

represented 10 miles of progress, and so on. As each wheel advances at

10 times the rate of the one to its left, so that after a complete

revolution of the one (i.e., by 10 units), the other will advance by

one unit, and vice versa. The odometer is thus a visual model of the

decimal numeration system, with each wheel corresponding to the place

value for a specific power of 10. In those days, since no one imagined

cars lasting for more than 100,000 miles, the odometer only had six

components, so that the left-most one corresponded to units of

10,000. But, of course, it is easy to imagine having arbitrarily more

wheels on the left to represent larger and larger whole numbers. More

interestingly, it is also easy to imagine adding wheels to the right,

even extending forever, making it possible to represent tinier and

tinier distances. It is also able to observe the change in the

odometer readings over fractional distances, like a 1/2 or 1/4 of a

mile, illustrating the decimal representation of fractions. The

concept of "carrying" is naturally illustrated by watching one or

(especially) more of the readings "turn over."

The odometer also illustrates the concepts of operators and

composition. Each of the wheels in the odometer is a kind of operator

which accepts input in the form of rotation and, except for the last,

in addition to a display, produces output in the form of a modified

rotation. The odometer itself is constructed as a composition of these

operators in which the output of each operator is connected as input

to the next. For the internal wheels, the effect of the operator is

that of the fraction one-tenth, which reduces the input by a factor of

10. The result of composing the operators is to successively reduce

the original input to one-tenth, one-hundredth, one-thousandth, and so

on, thus providing a visual representation of fractional

multiplication.

Other topics which can usefully be visualized in this

model include alternative bases (e.g., suppose our wheels use octal

units) and the relationship of speed, time, and distance. Now, we

can't subject students to endless hours of sitting in a car watching

an actual odometer. So, to make useful models, we need to simplify the

models and make the point of the models more explicit without

eliminating the element of discovery. So, our hope is to carry this

out for all kinds of visual interactive models and all kinds of

topics.

Please send questions, comments, and suggestions to:

david.posner@numbermodels.org

Models

Place Value

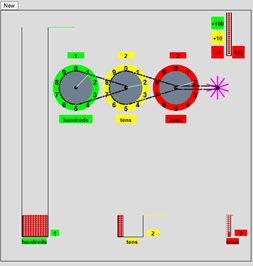
This model illustrates the concept of “place value” using “decimal

wheels”, represented as pulleys, and as quantities of balls. Balls

are loaded from a reservoir by clicking on buttons labeled “+1”,

“+10”, and “+100”. As the balls fall, they advance a paddle wheel

which drives the “ones” pulley one unit which drives the “tens” pulley

one tenth of a unit which drives the “hundreds” pulley one hundredth

of a unit. After this, the balls fall into a tube labeled “ones”.

When the tube is full of 10 balls, the tube of balls is moved into a

box of tubes in a container labeled “tens” and when this box is full

it is moved to a stack of boxes labeled “hundreds”. Counters track

the total number of balls loaded, the current place value of each

wheel, and the number of elements in each container. Clicking “new”

in the upper left corner resets the page.

Train Track Addition

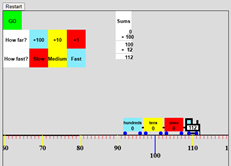
This model consists of a “railroad track” represented as a line marked off with unit tick marks having multiples of 10 and 100 distinguished by length and color, a train with cars labeled “hundreds”, “tens”, and “ones” which will specify how far the train is to travel on its next trip, buttons for setting the distance, a “GO” button for starting the train, buttons for setting the speed, and a column labeled “Sums” expressing the total distance traveled over multiple trips as a sequence of sums. The goal of the model is to illustrate several concepts including the use of position on a “number line” to represent numbers, the use of an intruction to change the location as an alternative model, and the sequencing of instructions as a model of addition. The duality of representations of number is common to models of number based on the state of a dynamic system, i.e., systems subject to change. In the first level a number is represented as a state of the system. At the next level number is represented as an instruction which causes the system state to change from the 0 state to the given state. The Addition “m+n” is thus represented as “execute m and then execute n”. For the model of number as a collection of objects “m+n” would be represented as “add m objects” and then “add n objects.” For the train system, m+n would be represented as “go a distance m” and then “go a distance n.” For the counting system “m+n” would be represented as “count the next m numbers” and then “count the next n numbers.” When we discuss multiplication, we will introduce a third level of interpretation of number: numbers as repeat operators.

Base 10 Addition:

Two Place Addition

Three Place Addition

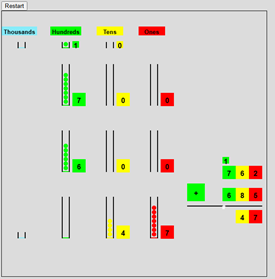
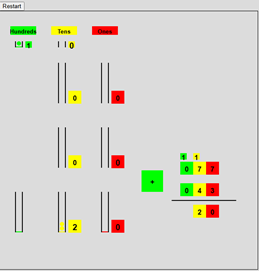
The purpose of this model is to teach and explain the base 10 addition procedure. When the models are run a random addition problem of the corresponding size is presented in the standard form together with a model consisting of quantities of balls, color coded by place value, for the digits of the summands. The steps of the procedure are carried out by clicking on the “+” button which changes color for the different place values. As the digits are added the balls for the corresponding place value drop into a collector with a counter showing the total. If the total reaches 10, the 10 balls are replaced with a ball which is moved to a “carry” holder for the next place value.